Skip to contents

Variability levels

Source: vignettes/v02_uncertainties.Rmd
v02_uncertainties.Rmd

Simulate with all variabilities

Let’s use a simple 1-compartment model with absorption compartment to illustrate the different levels of variabilities.

refModel <- model_suite$nonmem$advan2_trans2
refModel
## [MAIN]
## KA=THETA_KA*exp(ETA_KA)
## CL=THETA_CL*exp(ETA_CL)
## V=THETA_V*exp(ETA_V)
## S2=V
## 
## [ODE]
## d/dt(A_DEPOT)=-KA*A_DEPOT
## d/dt(A_CENTRAL)=-CL*A_CENTRAL/V + KA*A_DEPOT
## d/dt(A_OUTPUT)=CL*A_CENTRAL/V
## F=A_CENTRAL/S2
## 
## [ERROR]
## CONC=F
## CONC_ERR=CONC*(EPS_PROP + 1)
## 
## 
## THETA's:
##   name index value   fix
## 1   KA     1     1 FALSE
## 2   CL     2     5 FALSE
## 3    V     3    80 FALSE
## OMEGA's:
##   name index index2 value   fix type
## 1   KA     1      1 0.025 FALSE  var
## 2   CL     2      2 0.025 FALSE  var
## 3    V     3      3 0.025 FALSE  var
## SIGMA's:
##   name index index2 value   fix type
## 1 PROP     1      1 0.025 FALSE  var
## No variance-covariance matrix
## 
## Compartments:
## A_DEPOT (CMT=1)
## A_CENTRAL (CMT=2)
## A_OUTPUT (CMT=3)

We’re going to use a very basic dataset. 1000 mg QD shall be administered for a week.

ds <- Dataset(25) %>%
  add(Bolus(time=0, amount=1000, ii=24, addl=6)) %>%
  add(Observations(times=seq(0,24*7,by=4)))

All subjects are different due to IIV and RUV.

results <- refModel %>% simulate(dataset=ds, seed=1)
spaghettiPlot(results, "CONC_ERR")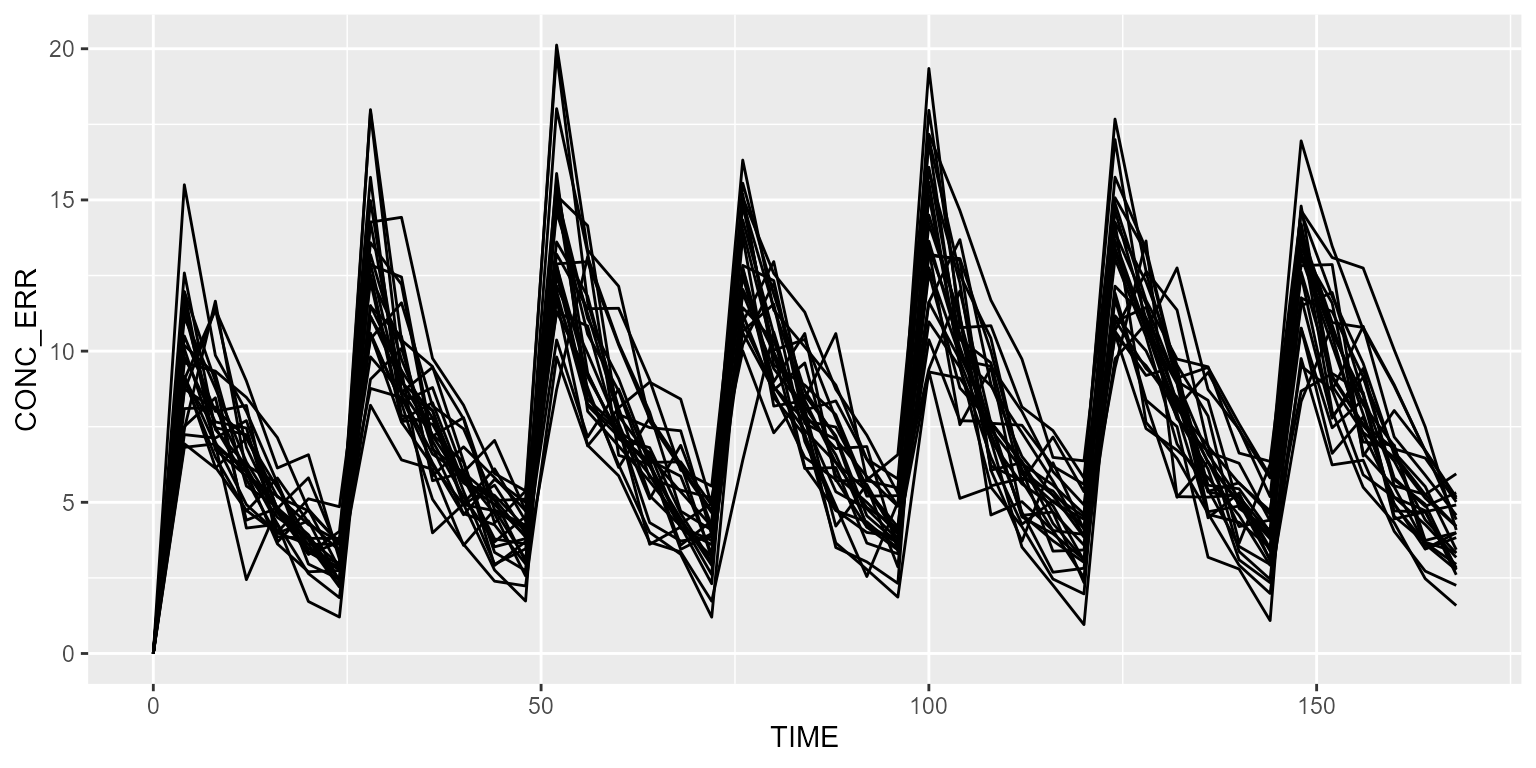

Simulate without RUV

Disabling RUV is done as follows:

model <- refModel %>% disable(c("RUV"))
model@parameters
## THETA's:
##   name index value   fix
## 1   KA     1     1 FALSE
## 2   CL     2     5 FALSE
## 3    V     3    80 FALSE
## OMEGA's:
##   name index index2 value   fix type
## 1   KA     1      1 0.025 FALSE  var
## 2   CL     2      2 0.025 FALSE  var
## 3    V     3      3 0.025 FALSE  var
## SIGMA's:
##   name index index2 value   fix type
## 1 PROP     1      1     0 FALSE  var
## No variance-covariance matrix

In that case, CONC_ERR (the observed concentration) is identical as CONC (the model-simulated plasma concentration).

results <- model %>% simulate(dataset=ds, seed=1)
spaghettiPlot(results, "CONC_ERR")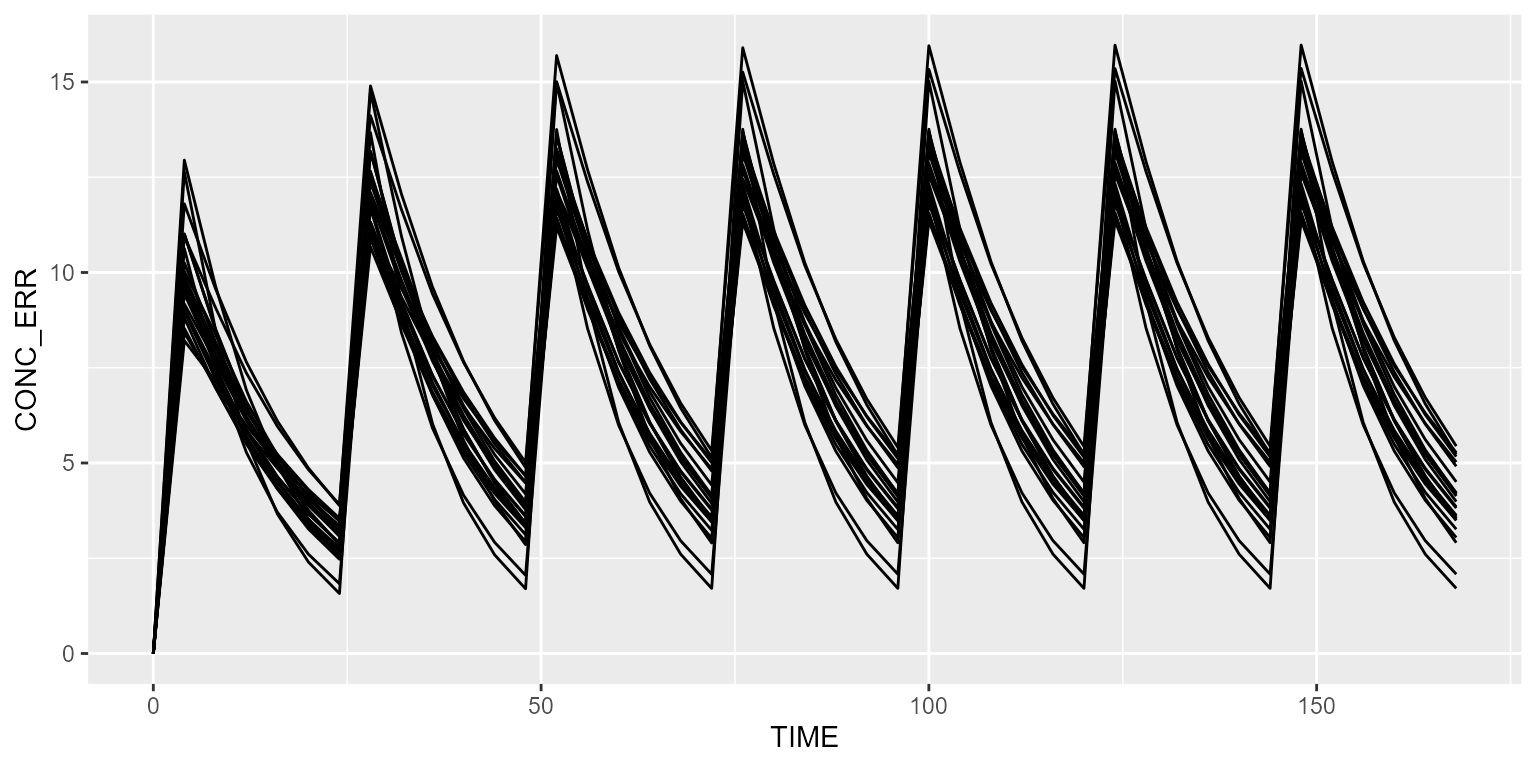

spaghettiPlot(results, "CONC")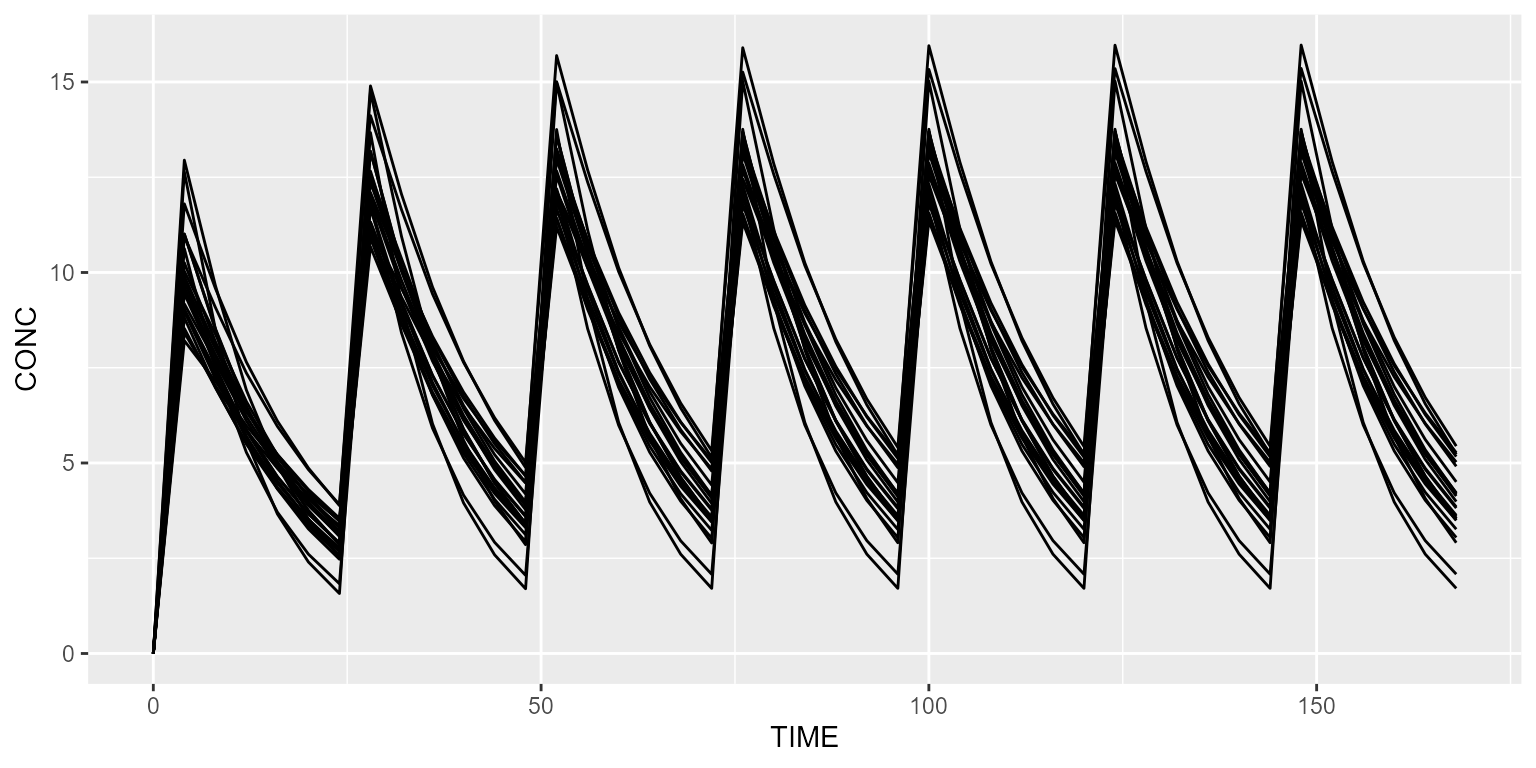

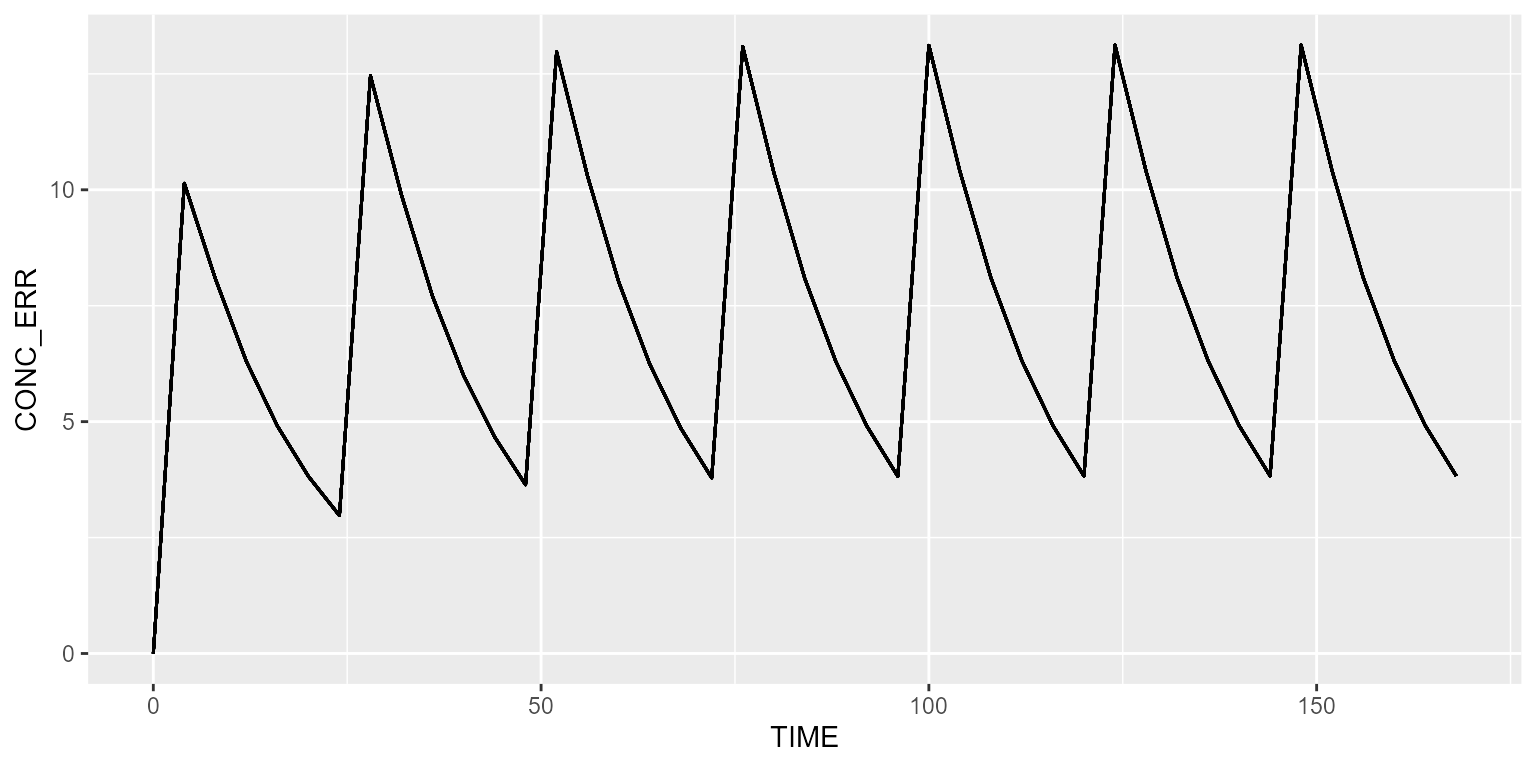
Simulate without RUV and IIV

Disabling RUV and IIV is done as follows:

model <- refModel %>% disable(c("IIV", "RUV"))
model@parameters
## THETA's:
##   name index value   fix
## 1   KA     1     1 FALSE
## 2   CL     2     5 FALSE
## 3    V     3    80 FALSE
## OMEGA's:
##   name index index2 value   fix type
## 1   KA     1      1     0 FALSE  var
## 2   CL     2      2     0 FALSE  var
## 3    V     3      3     0 FALSE  var
## SIGMA's:
##   name index index2 value   fix type
## 1 PROP     1      1     0 FALSE  var
## No variance-covariance matrix

Now, the typical profile is shown for all subjects.

results <- model %>% simulate(dataset=ds, seed=1)
spaghettiPlot(results, "CONC_ERR")