Complex PK/PD models from literature
Source:vignettes/v14_complex_pkpd_models.Rmd
v14_complex_pkpd_models.RmdThis vignette intends to demonstrate that CAMPSIS can be used to implement almost any PK/PD model, including complex ones.
Filgrastim PK/PD model
Load the filgrastim PK/PD model from the model library as follows. Please note that this model was translated from NONMEM code. The original model file can be found here on the DDMORE repository. Eventually, this model was updated with the final parameters from the corresponding publication (Krzyzanski et al., 2010).
pkpd <- model_suite$literature$filgrastim_pkpd_krzyzanski
pkpd## [MAIN]
## FF=THETA_FF
## KA=THETA_KA1*exp(ETA_KA1)
## FR=THETA_FR
## D2=THETA_D2
## KEL=THETA_KEL*exp(ETA_KEL)
## VD=THETA_VD*exp(ETA_VD)
## KD=THETA_KD
## KINT=THETA_KINT
## KSI=THETA_KSI*exp(ETA_KSI)
## KOFF=THETA_KOFF
## KMT=THETA_KMT
## KBB1=THETA_KBB1
## KTT=THETA_KTT
## NB0=THETA_NB0*exp(ETA_NB0)
## SC1=THETA_SC1*exp(ETA_SC1)
## SM1=THETA_SM1*exp(ETA_SM1)
## SM2=THETA_SM2*exp(ETA_SM2)
## SM3=THETA_SM3
## CP0=BAS
## F1=FF
## F2=0
## if (ROUT == 1) F1=0
## if (ROUT == 1) F2=1
## KON=KOFF/KD
## H10=CP0*SM1/(CP0 + SC1) + 1
## H20=CP0*SM2/(CP0 + SC1) + 1
## H30=CP0*SM3/(CP0 + SC1) + 1
## KINB=KMT*NB0/H10
## BM10=H10*KINB/(H20*KTT + H30*KBB1)
## BM20=BM10*H20*KTT/(H20*KTT + H30*KBB1)
## BM30=BM20*H20*KTT/(H20*KTT + H30*KBB1)
## BM40=BM30*H20*KTT/(H20*KTT + H30*KBB1)
## BM50=BM40*H20*KTT/(H20*KTT + H30*KBB1)
## BM60=BM50*H20*KTT/(H20*KTT + H30*KBB1)
## BM70=BM60*H20*KTT/(H20*KTT + H30*KBB1)
## BM80=BM70*H20*KTT/(H20*KTT + H30*KBB1)
## BM90=BM80*H20*KTT/(H20*KTT + H30*KBB1)
## NT0=BM10 + BM20 + BM30 + BM40 + BM50 + BM60 + BM70 + BM80 + BM90 + NB0
## AC0=CP0*VD
## RTOT0=KSI*NT0
## ADR0=AC0*RTOT0/(CP0 + KD)
## KIN=AC0*KEL + ADR0*KINT
##
## [ODE]
## ABS=A_1
## ATOT=A_2
## BM1=A_5
## BM2=A_6
## BM3=A_7
## BM4=A_8
## BM5=A_9
## BM6=A_10
## BM7=A_11
## BM8=A_12
## BM9=A_13
## NB=A_14
## NT=BM1 + BM2 + BM3 + BM4 + BM5 + BM6 + BM7 + BM8 + BM9 + NB
## RTOT=KSI*NT
## BB=-A_2/VD + KD + RTOT
## CP=-0.5*BB + 0.5*sqrt(4*A_2*KD/VD + pow(BB, 2))
## AC=CP*VD
## ADR=AC*RTOT/(CP + KD)
## H1=CP*SM1/(CP + SC1) + 1
## H2=CP*SM2/(CP + SC1) + 1
## H3=CP*SM3/(CP + SC1) + 1
## d/dt(A_1)=-ABS*KA
## d/dt(A_2)=ABS*KA - AC*KEL - ADR*KINT + KIN
## d/dt(A_3)=0
## d/dt(A_4)=0
## d/dt(A_5)=-BM1*H2*KTT - BM1*H3*KBB1 + BM1*H1*KINB/BM10
## d/dt(A_6)=BM1*H2*KTT - BM2*H2*KTT - BM2*H3*KBB1
## d/dt(A_7)=BM2*H2*KTT - BM3*H2*KTT - BM3*H3*KBB1
## d/dt(A_8)=BM3*H2*KTT - BM4*H2*KTT - BM4*H3*KBB1
## d/dt(A_9)=BM4*H2*KTT - BM5*H2*KTT - BM5*H3*KBB1
## d/dt(A_10)=BM5*H2*KTT - BM6*H2*KTT - BM6*H3*KBB1
## d/dt(A_11)=BM6*H2*KTT - BM7*H2*KTT - BM7*H3*KBB1
## d/dt(A_12)=BM7*H2*KTT - BM8*H2*KTT - BM8*H3*KBB1
## d/dt(A_13)=BM8*H2*KTT - BM9*H2*KTT - BM9*H3*KBB1
## d/dt(A_14)=BM9*H2*KTT + H3*KBB1*(BM1 + BM2 + BM3 + BM4 + BM5 + BM6 + BM7 + BM8 + BM9) - KMT*NB
##
## [F]
## A_1=F1
## A_2=F2
##
## [DURATION]
## A_2=D2
##
## [INIT]
## A_1=0
## A_2=AC0 + ADR0
## A_3=0
## A_4=0
## A_5=BM10
## A_6=BM20
## A_7=BM30
## A_8=BM40
## A_9=BM50
## A_10=BM60
## A_11=BM70
## A_12=BM80
## A_13=BM90
## A_14=NB0
##
##
## THETA's:
## name index value fix
## 1 FF 1 0.60200 FALSE
## 2 KA1 2 0.65100 FALSE
## 3 FR 3 1.00000 TRUE
## 4 D2 4 0.50000 TRUE
## 5 KEL 5 0.15200 FALSE
## 6 VD 6 2.42000 FALSE
## 7 KD 7 1.44000 FALSE
## 8 KINT 8 0.10500 FALSE
## 9 KSI 9 0.18100 FALSE
## 10 KOFF 10 0.00000 TRUE
## 11 KMT 11 0.07280 FALSE
## 12 KBB1 12 0.00000 TRUE
## 13 KTT 13 0.00862 FALSE
## 14 NB0 14 1.55000 FALSE
## 15 SC1 15 3.15000 FALSE
## 16 SM1 16 34.70000 FALSE
## 17 SM2 17 32.20000 FALSE
## 18 SM3 18 0.00000 TRUE
## OMEGA's:
## name index index2 value fix type
## 1 NB0 1 1 0.109000 FALSE var
## 2 KEL 2 2 0.194000 FALSE var
## 3 VD 3 3 0.138000 FALSE var
## 4 KA1 4 4 0.000000 TRUE var
## 5 KSI 5 5 0.058700 FALSE var
## 6 SC1 6 6 0.764000 FALSE var
## 7 SM1 7 7 0.000188 FALSE var
## 8 SM2 8 8 0.000000 TRUE var
## SIGMA's:
## # A tibble: 0 × 0
## No variance-covariance matrix
##
## Compartments:
## A_1 (CMT=1)
## A_2 (CMT=2)
## A_3 (CMT=3)
## A_4 (CMT=4)
## A_5 (CMT=5)
## A_6 (CMT=6)
## A_7 (CMT=7)
## A_8 (CMT=8)
## A_9 (CMT=9)
## A_10 (CMT=10)
## A_11 (CMT=11)
## A_12 (CMT=12)
## A_13 (CMT=13)
## A_14 (CMT=14)Let’s create a simple demonstration dataset of 250 subjects:
baseDataset <- Dataset(250) %>%
add(Covariate("BAS", 0.02)) %>%
add(Covariate("WT", UniformDistribution(50, 100))) %>%
add(DoseAdaptation("WT*AMT")) %>% # per kilo dosing
add(Observations(0:216)) %>%
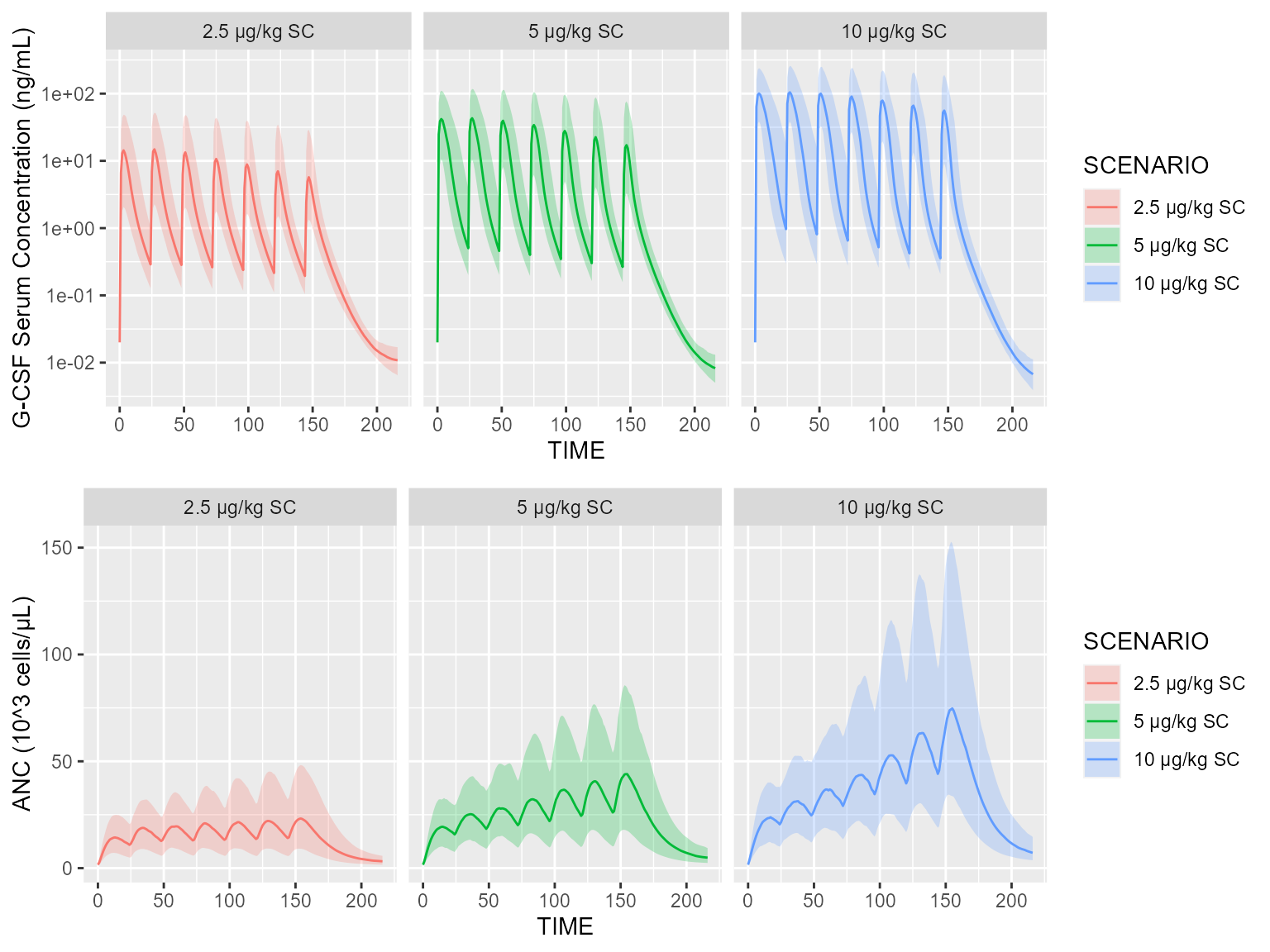
add(Covariate("ROUT", 0)) # subcutaneous route (SC)Assume we want to compare the following subcutaneous administrations of filgrastim:
- 2.5 μg/kg QD for a week
- 5 μg/kg QD for a week
- 10 μg/kg QD for a week
We define the following scenarios:
scenarios <- Scenarios() %>%
add(Scenario("2.5 μg/kg SC", dataset=~.x %>% add(Bolus(time=0, amount=2.5, compartment=1, ii=24, addl=6)))) %>%
add(Scenario("5 μg/kg SC", dataset=~.x %>% add(Bolus(time=0, amount=5, compartment=1, ii=24, addl=6)))) %>%
add(Scenario("10 μg/kg SC", dataset=~.x %>% add(Bolus(time=0, amount=10, compartment=1, ii=24, addl=6))))A quick simulation gives us the plasma concentration of filgrastim, as well as the absolute neutrophil count (ANC):
library(ggplot2)
results <- pkpd %>% simulate(dataset=baseDataset, scenarios=scenarios, seed=1)
results <- results %>% dplyr::mutate(SCENARIO=factor(SCENARIO, levels=unique(SCENARIO)))
p1 <- shadedPlot(results, "CP", "SCENARIO") + facet_wrap(~SCENARIO) +
scale_y_log10(breaks=c(.01,.1,1,10,100)) + ylab("G-CSF Serum Concentration (ng/mL)")
p2 <- shadedPlot(results, "A_14", "SCENARIO") + facet_wrap(~SCENARIO) +
ylab("ANC (10^3 cells/μL)")
gridExtra::grid.arrange(p1, p2, nrow=2)